رمزنگاری RSA چیست؟

رمزنگاری RSA چیست؟، رمزنگاری RSA یک رمزگذاری نامتقارن است که به دلیل سهولت کاربری در انتقال داده های آنلاین استفاده می شود. RSA از یک کلید عمومی و یک کلید خصوصی تشکیل شده است. کلید عمومی جهت رمزگذاری و همتای خصوصی آن برای رمزگشایی استفاده می شود. از آنجایی که هیچ الگوریتمی وجود ندارد که بتواند کلید خصوصی را از کلید عمومی تعیین نماید، این روش امن در نظر گرفته می شود. علاوه بر رمزگذاری، سیستم رمزنگاری RSA جهت تولید امضای دیجیتال نیز مناسب است.
 

فهرست

1. رمزنگاری RSA چیست؟
2. رمزگذاری RSA کجا استفاده می شود؟
3. عملکردهای تابع دریچه ای
4. تولید اعداد اول
5. تولید کلید عمومی
6. تولید کلید خصوصی
7. امنیت و حملات RSA
8. بنابراین، مشکل RSA چیست؟

رمزنگاری RSA چیست؟

RSA مخفف Rivest-Shamir-Adleman، نام خانوادگی سازندگان آن است. قبل از رمزگذاری کلید عمومی، چنانچه از قبل فرصتی چهت مبادله ایمن کلیدها وجود نداشت، برقراری ارتباط ایمن یک چالش بود. اگر فرصتی برای به اشتراک گذاشتن کلید پیش از موعد وجود نداشت، یا یک کانال امن که بتوان از طریق آن کلیدها را توزیع نمود، هیچ راهی جهت برقراری ارتباط بدون تهدید دشمنان قادر به رهگیری و دسترسی به محتوای پیام وجود نداشت.

تا دهه 1970 بود که اوضاع واقعاً شروع به تغییر کرد. اولین پیشرفت عمده در جهت آنچه که ما اکنون رمزنگاری کلید عمومی می نامیم در آغاز دهه توسط جیمز اچ الیس منتشر شد. الیس نتوانست راهی برای اجرای کار خود بیابد، اما همکارش کلیفورد کاکس آن را گسترش داد تا به چیزی تبدیل شود که ما اکنون به عنوان رمزگذاری RSA می شناسیم.

آخرین قطعه پازل چیزی است که ما اکنون آن را تبادل کلید دیفی هلمن Diffie-Hellman می نامیم. مالکوم جی ویلیامسون، همکار دیگر، طرحی را کشف کرد که به دو طرف اجازه می داد یک کلید رمزگذاری را به اشتراک بگذارند، حتی اگر کانال توسط دشمنان تحت نظارت باشد.

همه این کارها در آژانس اطلاعاتی بریتانیا، ستاد ارتباطات دولتی (GCHQ) انجام شد و این کشف را طبقه بندی نمود. تا حدی به دلیل محدودیت‌ های تکنولوژیکی، GCHQ در آن زمان نمی‌توانست کاربرد رمزنگاری کلید عمومی را مشاهده نماید، بنابراین توسعه آن مسکوت ماند. تا اینکه در سال 1997 کار از طبقه بندی خارج شد و مخترعان اصلی RSA شناخته شدند.

چندین سال بعد، مفاهیم مشابه در حوزه عمومی شروع به توسعه کردند. رالف مرکل شکل اولیه رمزنگاری کلید عمومی را ایجاد نمود که بر ویتفیلد دیفی و مارتین هلمن در طراحی تبادل کلید دیفی-هلمن تأثیر گذاشت.

ایده‌های دیفی و هلمن یکی از جنبه‌های مهمی را که کار آن‌ها را به پایه‌ای از رمزنگاری کلید عمومی تبدیل می‌کرد، از دست داده بودند. در واقع ایده یک تابع یک طرفه بود که معکوس کردن آن دشوار بود. در سال 1977، ران ریوست، آدی شامیر و لئونارد ادلمن، که نام خانوادگی آنها مخفف RSA است، پس از یک سال کار بر روی این مشکل، راه حلی ارائه کردند.

ایده ریوست در سال 1983 توسط MIT به ثبت رسید، اما در روزهای اولیه اینترنت بود که الگوریتم RSA شروع به پذیرش گسترده به عنوان یک ابزار امنیتی مهم کرد.

ران ریوست، آدی شامیر و لئونارد ادلمن در سال 1977 تصمیم گرفتند که این کار را انجام دهند. سرانجام پس از چندین رویکرد ناموفق (و با تمام امید از دست رفته)، آنها به فاکتورسازی اولیه به عنوان روشی جهت رمزگذاری یک طرفه دست یافتند.

مهمترین ویژگی رمزنگاری نامتقارن این است که برای مثال یک فایل جهت رمزگشایی مجدد وجود ندارد، بلکه دو کلید وجود دارد. در رمزنگاری RSA، یک کلید عمومی وجود دارد که آزادانه در دسترس تمامی نود ها می باشد، و یک کلید خصوصی که ترجیحاً باید فقط برای یک شخص قابل تشخیص و شناخته شود. رمزگذاری اصلی با کلید عمومی RSA انجام می شود. با این حال، کلید خصوصی RSA جهت رمزگشایی مورد نیاز است. اگر کلید گم شود، رمزنگاری در واقع نمی تواند شکسته شود.

اساس سیستم رمزنگاری RSA تابع دریچه ای trapdoor function است که از ریاضیات شناخته شده است. این بیان می کند که یک تابع تنها در صورتی می تواند معکوس شود که اطلاعات اضافی معرفی شود. اگر این اطلاعات ارائه نشود، متغیرهای زیادی وجود دارد، به این معنی که یک راه حل را نمی توان در یک چارچوب زمانی واقعی محاسبه کرد. در مورد سیستم رمزنگاری RSA، کلید خصوصی RSA حاوی این اطلاعات اضافی است.

تحت رمزگذاری RSA، پیام‌ها با کدی به نام کلید عمومی رمزگذاری می‌شوند که می‌توان آن را به صورت آزاد به اشتراک گذاشت. با توجه به برخی ویژگی‌های ریاضی متمایز الگوریتم RSA، هنگامی که یک پیام با کلید عمومی رمزگذاری شد، تنها می‌توان آن را توسط کلید دیگری به نام کلید خصوصی رمزگشایی کرد. هر کاربر RSA دارای یک جفت کلید متشکل از کلیدهای عمومی و خصوصی است. همانطور که از نام آن پیداست، کلید خصوصی باید مخفی بماند.

رمزگذاری RSA کجا استفاده می شود؟

رمزگذاری RSA اغلب در ترکیب با سایر طرح های رمزگذاری یا برای امضاهای دیجیتالی استفاده می شود که می تواند صحت و یکپارچگی یک پیام را ثابت نماید. معمولاً جهت رمزگذاری کل پیام‌ها یا فایل‌ها استفاده نمی‌شود، چراکه نسبت به رمزگذاری با کلید متقارن کارایی کمتر و منابع سنگین‌تری دارد.

برای کارآمدتر کردن کارها، یک فایل به طور کلی با یک الگوریتم کلید متقارن رمزگذاری می شود و سپس کلید متقارن با رمزگذاری RSA رمزگذاری می شود. تحت این فرآیند، تنها موجودی که به کلید خصوصی RSA دسترسی دارد، می‌تواند کلید متقارن را رمزگشایی کند.

بدون دسترسی به کلید متقارن، فایل اصلی را نمی توان رمزگشایی نمود. از این روش می توان برای ایمن نگه داشتن پیام ها و فایل ها، بدون صرف زمان زیاد یا مصرف بیش از حد منابع محاسباتی استفاده کرد.

رمزگذاری RSA را می توان در تعدادی از سیستم های مختلف استفاده نمود. می توان آن را در OpenSSL، wolfCrypt، cryptlib و تعدادی دیگر از کتابخانه های رمزنگاری پیاده سازی کرد.

به عنوان یکی از اولین طرح های رمزگذاری کلید عمومی که به طور گسترده مورد استفاده قرار گرفت، RSA پایه بسیاری از ارتباطات ایمن ما را پایه گذاری نمود. به طور سنتی در TLS استفاده می شد و همچنین الگوریتم اصلی مورد استفاده در رمزگذاری PGP بود. RSA هنوز در طیف وسیعی از مرورگرهای وب، ایمیل، VPN ها، چت و سایر کانال های ارتباطی دیده می شود.

RSA همچنین اغلب برای ایجاد ارتباطات ایمن بین مشتریان VPN و سرورهای VPN استفاده می شود. تحت پروتکل هایی مانند OpenVPN، دست دادن TLS می تواند از الگوریتم RSA برای تبادل کلیدها و ایجاد یک کانال امن استفاده کند.

عملکردهای تابع دریچه ای trapdoor function

رمزگذاری RSA با این فرض کار می کند که محاسبه الگوریتم در یک جهت آسان است، اما در معکوس تقریبا غیرممکن است. به عنوان مثال، اگر به شما گفته شود که 701111 حاصل ضرب دو عدد اول است، آیا می توانید پی ببرید که آن دو عدد چیست؟

حتی با یک ماشین حساب یا یک کامپیوتر، اکثر ما نمی‌دانیم از کجا شروع کنیم، چه رسد به اینکه بتوانیم پاسخ را بفهمیم. اما اگر همه موضوعی را دور بزنیم، خیلی راحت تر می شود. نتیجه چیست:

907 x 773

چنانچه به اندازه کافی حوصله داشتید، می توانستید تلفن خود را بیرون بیاورید یا شاید آن را در ذهن خود محاسبه نمایید تا متوجه شوید که پاسخ همان 701111 است که قبلا ذکر شد. اعداد 907 و 773 اعداد اولی هستند که به اولین سوال ما پاسخ می‌دهند، که به ما نشان می‌دهد که به راحتی می‌توان معادلات خاصی را از یک طرف به‌دست آورد، اما در حالت معکوس به ظاهر غیرممکن است.

یکی دیگر از جنبه های جالب این معادله این است که اگر یکی از اعداد اول را داشته باشید و همچنین نتیجه حاصلضرب را، محاسبه ساده ای دارید. اگر به شما گفته شود که 701111 حاصل ضرب 907 در عدد اول دیگر است، می توانید عدد اول دیگر را با معادله زیر بدست آورید:

701,111 ÷ 907 = 773

از آنجایی که محاسبه رابطه بین این اعداد در یک جهت ساده است، اما در معکوس فوق العاده دشوار، این معادله به عنوان تابع دریچه ای شناخته می شود. توجه داشته باشید که در حالی که درک مثال بالا برای عموم سخت است، کامپیوترها می توانند این عملیات را در زمان کمی انجام دهند.

به همین دلیل، RSA از اعداد بسیار بزرگتری استفاده می نماید. اندازه اعداد اول در پیاده سازی RSA واقعی متفاوت است، اما در RSA 2048 بیتی، آنها جهت ساخت کلیدهایی با طول 617 رقم گرد هم می آیند. برای کمک به تجسم آن، یک کلید می تواند تعدادی به این اندازه باشد:


999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

تولید اعداد اول

توابع دریچه ای که در بالا ذکر شد، اساس نحوه عملکرد طرح های رمزگذاری کلید عمومی و خصوصی را تشکیل می دهند. ویژگی‌های آن‌ها اجازه می‌دهد کلیدهای عمومی بدون به خطر انداختن پیام یا فاش شدن کلید خصوصی به اشتراک گذاشته شوند. آنها همچنین اجازه می دهند داده ها با یک کلید به گونه ای رمزگذاری شوند که فقط توسط کلید دیگر جفت رمزگشایی شود.

[اعداد اول Prime numbers – اعدادی بزرگتر از یک هستند که فقط بر یک و خودشان (عوامل) بخش پذیرند.]

اولین مرحله رمزگذاری یک پیام با RSA، تولید کلیدها است. برای این کار به دو عدد اول (p و q) نیاز داریم که با تست primality انتخاب می شوند. تست اولیه الگوریتمی است که به طور موثر اعداد اول را پیدا می کند، مانند تست اولیه رابین-میلر.

اعداد اول در RSA البته بایستی بسیار فراتر و همچنین نسبتاً دور از هم باشند. شکستن اعدادی که کوچکتر یا نزدیکتر هستند بسیار ساده تر است. با این وجود،  در مثال ما از اعداد کوچکتر استفاده می شود تا کار را آسان تر دنبال کنیم و محاسبه ساده تری داشته باشیم.

فرض کنید که تست اولیه اعداد اولی را که در بالا استفاده کردیم، 907 و 773 را به ما می دهد. مرحله بعدی بدست آوردن مقدار (n) با استفاده از فرمول زیر است:

n = p x q

جایی که p = 907 و q = 773

از این رو:

n = 907 x 773

n = 701,111

تابع کلی کارمایکل

هنگامی که n را داشته باشیم، از تابع کارمایکل استفاده می کنیم:

 λ(n) = lcm (p − 1, q − 1)

برای کسانی که آگاه نیستند، λ(n) نشان دهنده تابع کارمایکل برای n است، در حالی که lcm به معنای پایین ترین مضرب مشترک است، که کمترین عددی است که هم p و هم q می توانند به آن تقسیم شوند. چند راه مختلف برای فهمیدن این موضوع وجود دارد، اما ساده‌ترین راه این است که به یک ماشین حساب اعتماد کنید تا معادله را برای شما انجام دهد. پس بیایید اعداد خود را در معادله قرار دهیم:

λ(701,111) = lcm (907 − 1, 773 − 1)

 λ(701,111) = lcm (906, 772)

 λ(701,111) = 349,716

تولید کلید عمومی

اکنون که مقدار کارمایکل از اعداد اول خود را داریم، زمان آن رسیده است که کلید عمومی خود را بدست آوریم. تحت RSA، کلیدهای عمومی از یک عدد اول e و همچنین مقدار n تشکیل شده اند (ما در چند پاراگراف توضیح خواهیم داد که مقدار به چه معناست). عدد e می تواند چیزی بین 1 و مقدار λ(n) باشد که در مثال ما 349716 است.

از آنجایی که کلید عمومی به صورت باز به اشتراک گذاشته می شود، چندان مهم نیست که e یک عدد تصادفی باشد. در عمل، e به طور کلی روی 65537 تنظیم می شود، چراکه زمانی که اعداد بسیار بزرگتر به طور تصادفی انتخاب می شوند، رمزگذاری را بسیار کارآمدتر می نماید. برای مثال، ما اعداد را کوچک نگه می‌داریم تا محاسبات را کارآمد کنیم. بیایید بگوییم:

e = 11

داده های رمزگذاری شده نهایی ما متن رمز شده (c) نامیده می شود. ما آن را از پیام متنی ساده خود (m)، با اعمال کلید عمومی با فرمول زیر استخراج می کنیم:

c = m^e mod n

همانطور که اشاره کردیم،^e mod n کلید عمومی است. ما قبلا e را طراحی کرده ایم و n را نیز می شناسیم. تنها چیزی که باید توضیح دهیم، mod است. کمی از عمق این مقاله خارج است، اما به یک عملیات مقدار اشاره دارد، که در اصل به معنای باقیمانده هنگام تقسیم یک طرف به طرف دیگر است. مثلا:

10 mod 3 = 1

عدد 1 به این دلیل است که 3 سه بار در 10 تکرار می شود، با باقیمانده 1.

بازگشت به معادله ما. جهت ساده نگه داشتن همه مطالب، فرض کنید که پیام (m) که می‌خواهیم رمزگذاری کنیم و مخفی نگه داریم، فقط یک عدد است، 4. بیایید همه چیز را وصل کنیم:

c = m^e mod n

c = 4¹¹ mod 701,111

c = 4,194,304 mod 701,111

باز هم، برای آسان ساختن عملیات، ما از یک ماشین حساب استفاده خواهیم کرد، اما شما می توانید خودتان آن را متوجه شوید. با وارد کردن 4,194,304 در ماشین حساب، جواب دریافتی:

c = 688,749

بنابراین وقتی از RSA برای رمزگذاری پیام خود، 4، با کلید عمومی خود استفاده می کنیم، متن رمزی 688749 را به ما می دهد. مراحل قبلی ممکن است کمی بیش از حد با ریاضی دشوار به نظر رسد، اما مهم است که آنچه را که واقعاً اتفاق افتاده است تکرار کنید.

ما یک پیام 4 داشتیم که می خواستیم آن را مخفی نگه داریم. ما یک کلید عمومی برای آن اعمال کردیم که نتیجه رمزگذاری شده 688749 را به ما داد. اکنون که رمزگذاری شده است، می توانیم شماره 688749 را به طور ایمن برای دارنده جفت کلید ارسال نماییم. او تنها فردی می باشد که می توانند آن را با کلید خصوصی خود رمزگشایی کند. وقتی آن را رمزگشایی می کند، پیامی را می بینند که ما واقعاً ارسال می کردیم، 4.

تولید کلید خصوصی

در رمزگذاری RSA، هنگامی که داده یا پیامی با یک کلید عمومی به متن رمزی تبدیل شد، تنها می‌تواند توسط کلید خصوصی از همان جفت کلید رمزگشایی شود. کلیدهای خصوصی از d و n تشکیل شده اند. ما قبلاً n را می دانیم و از معادله زیر برای یافتن d استفاده می شود:

d =1/e mod λ(n)

در بخش ایجاد کلید عمومی در بالا، ما قبلاً تصمیم گرفتیم که در مثال خود، e برابر با 11 باشد. به طور مشابه، می‌دانیم که λ(n) برابر با 349716 فرایند قبلی ما تحت تابع totient کارمایکل است. وقتی با این بخش از فرمول مواجه می شویم، همه چیز کمی پیچیده تر می شود:

1/e mod

این معادله ممکن است به نظر برسد که از شما می خواهد 1 را بر 11 تقسیم کنید، اما اینطور نیست. در عوض، تنها نشان می دهد که ما باید معکوس مقدار e (که در این مورد 11 است) و λ(n) (که در این مورد 349716 است) را محاسبه کنیم.

در اصل بدین گونه است که به جای اجرای یک عملیات مقدار استاندارد، از معکوس عدد استفاده خواهیم نمود. فرایند معمولاً با الگوریتم اقلیدسی(وابسته به هندسه اقلیدس) توسعه یافته می شود، البته کمی خارج از محدوده این مقاله است، بنابراین ما فقط تقلب می کنیم و به جای آن از یک ماشین حساب استفاده می کنیم. اکنون که همه چیز را درک می کنیم، بیایید اطلاعات خود را در فرمول وارد نماییم:

d =1/11 mod 349,716

جهت انجام این عملیات، به سادگی عدد 11 را وارد کنید (یا هر مقداری را که ممکن است برای e داشته باشید، اگر با مثال خودتان این کار را انجام می دهید) جایی که عدد صحیح و 349716 را نشان می دهد (یا هر مقداری که ممکن است برای λ(n) داشته باشید، اگر این کار را انجام می دهید. با مثال خودتان) جایی که در ماشین حساب که در بالا گفته شد و اگر آن را به درستی انجام داده اید، باید به نتیجه ای برسید که:

d = 254, 339

اکنون که مقدار d را داریم، می‌توانیم پیام‌هایی را که با کلید عمومی ما رمزگذاری شده‌اند، با استفاده از فرمول زیر رمزگشایی کنیم:

m = c^d mod n

اکنون می‌توانیم به متن رمزی که در بخش Generating the private key رمزگذاری کرده‌ایم برگردیم. وقتی پیام را با کلید عمومی رمزگذاری کردیم، مقدار c برابر با 688749 گردید. از بالا می دانیم که d برابر با 254339 است. همچنین می دانیم که n برابر با 701111 است. در نتیجه:

m = 688,749^254,339 mod 701,111.

همانطور که ممکن است متوجه شده باشید، تلاش جهت رساندن یک عدد به توان 254339 ممکن است برای اکثر ماشین‌ حساب‌های معمولی کمی سخت باشد. در عوض، ما از یک ماشین حساب رمزگشایی RSA استفاده خواهیم نمود. اگر می‌خواهید از روش دیگری استفاده نمایید، قدرت‌ها را مانند حالت عادی اعمال می‌کنید و عملیات  را به همان روشی که در بخش Generating the public انجام دادیم، پیش می بریم.

در ماشین‌ حساب لینک زیر، 701111 را وارد کنید، جایی که عبارت Supply Modulus: N، 254399 را در جایی که می‌گوید کلید رمزگشایی: D، و 688749 را در جایی که پیام رمز متنی را به شکل عددی می‌گوید، وارد کنید، همانطور که در زیر نشان داده شده است:

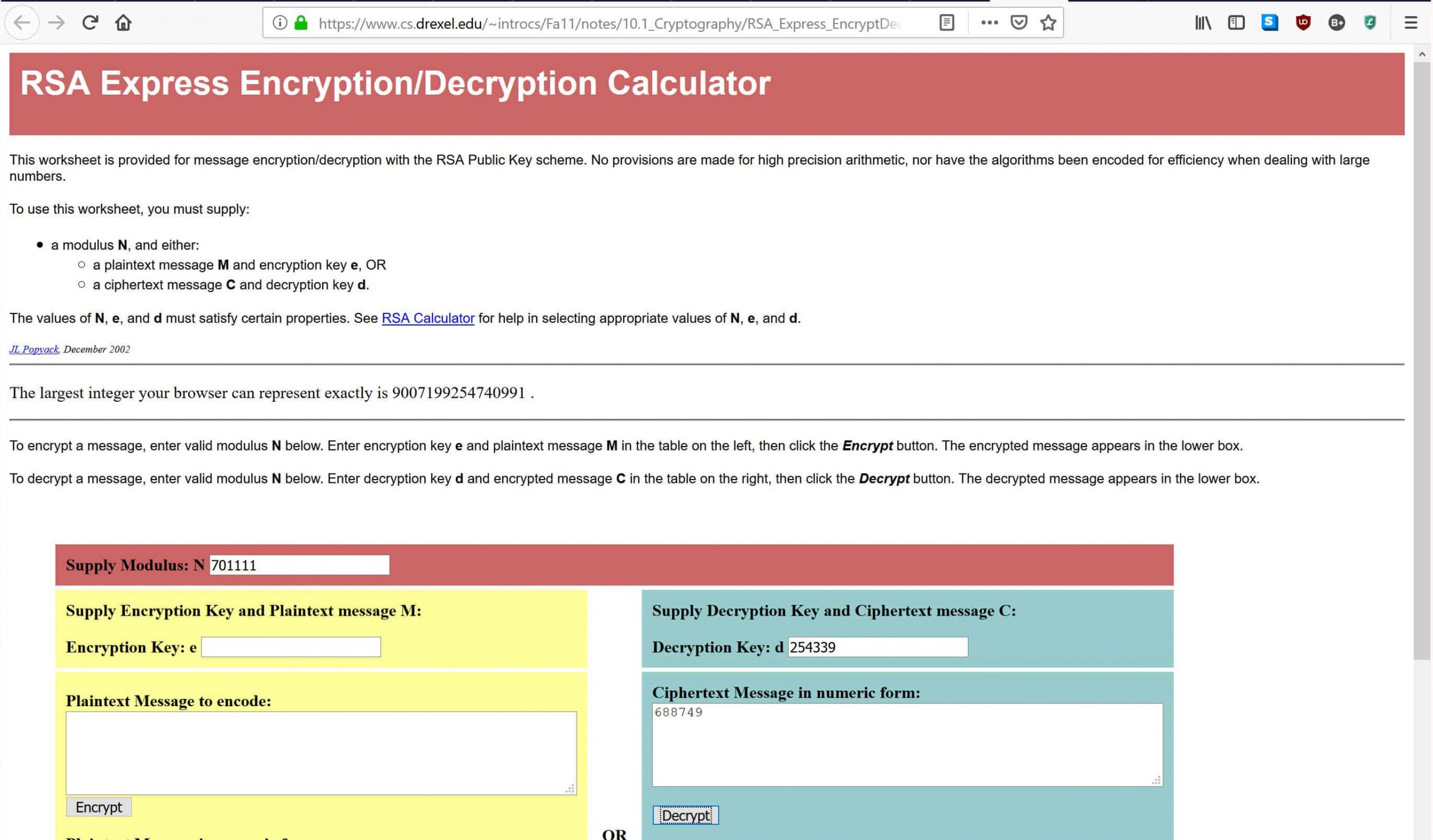
هنگامی که داده ها را وارد نمودید، Decrypt را بزنید، که اعداد را از طریق فرمول رمزگشایی که در بالا ذکر شد قرار می دهد. عملیات به شما پیام اصلی را در کادر زیر می دهد. اگر همه کارها را به درستی انجام داده اید، باید پاسخ 4 را دریافت کنید که همان پیام اصلی بود که ما با کلید عمومی خود رمزگذاری کردیم.

 p * q = n

λ(n) = lcm (p − 1, q − 1)

c = m^e mod n

 10mod 3 = 1

d =1/e mod λ(n)

m = c^d mod n

هر کسی می‌تواند کلید عمومی را بگیرد و از آن برای رمزگذاری یک داده استفاده نماید. به طور معمول در زمینه SSL/TLS چیزی که رمزگذاری می شود، کلید نشست Session است. با این حال، بدون دانستن مقادیر دو عدد اول، p و q، هیچ کس دیگری نمی تواند پیام را رمزگشایی نماید.

برای اینکه درک بهتری از سختی محاسباتی RSA داشته باشید، فاکتورسازی یک عدد 232 رقمی برای گروهی از محققین بیش از 1500 سال زمان محاسباتی (که در صدها کامپیوتر توزیع شده است) طول خواهد کشید.

کلیدهای RSA چگونه استفاده می شوند؟

یک سیستم رمزنگاری RSA می تواند جهت تبدیل داده ها، متن یا حتی یک تصویر به همراه یک الگوریتم غیرقابل تشخیص استفاده شود. بدون کلید خصوصی RSA، فایل مربوطه غیرقابل خواندن باقی می ماند و نه با چشم غیر مسلح رمزگشایی می شود و نه توسط برنامه رمزگشایی می شود. داده های اساسی ابتدا به اعداد طبیعی تبدیل می شوند و سپس با استفاده از کلید عمومی RSA رمزگذاری می شوند. کلید عمومی و خصوصی RSA از یک جفت اعداد تشکیل شده است که در هر مورد یکی از دو عدد یکسان است. این عدد ماژول RSA نامیده می شود.

دو عدد باقیمانده را توان رمزگذاری و توان رمزگشایی می نامند. آنها از اعداد اول تصادفی انتخاب شده تشکیل می شوند که تقریباً مقیاس یکسانی دارند اما نباید خیلی به هم نزدیک باشند. سپس اعداد با استفاده از فرمول های ریاضی محاسبه می شوند. فرآیند رمزگذاری برای عموم در دسترس است و بنابراین به راحتی می توان آن را بازتولید کرد. با این حال، برای خوانایی مجدد متن رمزگذاری شده، علاوه بر کلید عمومی، به کلید RSA خصوصی نیز نیاز است. تا به حال، هیچ الگوریتمی وجود نداشته است که به طور قابل اعتماد یک عدد را به فاکتورهای اول آن تجزیه نماید.

به طور معمول، طول کلید چیزی است که دشواری محاسبات را نشان می دهد. در حال حاضر استاندارد کلیدهای RSA 2048 بیتی است که از 1024 بیت که تا همین چند سال پیش مجاز بود افزایش یافته است. برخی از سازمان ها از کلیدهای 3072 بیتی و 4096 بیتی استفاده می نمایند، اما با افزایش اندازه کلیدهای RSA، میزان امنیت ارائه شده توسط آنها متناسب با میزان توان محاسباتی مورد نیاز جهت استفاده از آنها نیست.

بنابراین، مشکل RSA چیست؟

خوب، جدا از این واقعیت که مقیاس ضعیفی دارد، پاشنه آشیل برای RSA این است که برای تعیین اعداد اول (p و q) به مولدهای اعداد تصادفی متکی است.

یک مولد اعداد تصادفی (RNG) در واقع فقط یک دستگاه یا برنامه است که دنباله ای از اعداد را تولید می نماید که با احتمالی بیشتر از شما به صورت تصادفی قابل پیش بینی نیستند. از این رو نام.

از دیدگاه RSA، اعداد تصادفی یا RNG ها دو مشکل بزرگ دارند:

1. آنها صد در صد تصادفی نیستند
2. تقریباً همه از همان ها استفاده می کنند

برای تمامی مقاصد، دو راه جهت تولید اعداد تصادفی وجود دارد. اولی از شما می‌خواهد که یک رویداد یا پدیده طبیعی را که انتظار می‌رود تصادفی باشد، ترسیم نمایید. در واقع یک روش نسبتاً جدید تولید کلید بیولوژیکی در دانشگاه ایالتی پن آزمایش شده است که حرکت سلول‌های زنده را در برابر شبکه‌ای که روی آن قرار گرفته است ترسیم می نماید و سپس از آن برای تولید یک کلید رمزنگاری استفاده می‌کند. Cloudflare کاری مشابه با لامپ های گدازه ای در لابی خود انجام می دهد.

صادقانه بگویم، راه اول به نوعی جذاب است. روش دوم تولید اعداد شبه تصادفی نامیده می شود و متکی بر الگوریتم های محاسباتی است. به‌خاطر رمزگذاری RSA، ما این تولید کننده‌ های اعداد شبه تصادفی امن رمزنگاری‌ شده را (CSPRNG) می‌نامیم که توالی‌ های طولانی از نتایج تصادفی را تولید می‌کنند که در واقع کاملاً بر اساس یک مقدار کوتاه‌تر به نام دانه seed تعیین می‌شوند.

در اینجا لیستی از برخی از رایج ترین CSPRNG های مورد استفاده که استاندارد شده اند آمده است:

1. FIPS 186-4
2. NIST SP 800-900A Rev. 1
3. ANSI X9.17-1985 ضمیمه C
4. ANSI X9.31-1998 پیوست A.2.4
5. ANSI X9.62-2005، پیوست D

این عدم تنوع دانه ها به اولین مسئله ای که RSA دارد برمی گردد: اعداد اولی که تولید می شوند واقعاً تصادفی نیستند.

سیستم های رمزگذاری RSA برای چه مواردی استفاده می شوند؟

رمزگذاری RSA در بسیاری از زمینه‌های زندگی دیجیتالی روزمره استفاده می‌شود. به عنوان مثال، پروتکل ارتباطی HTTPS (پروتکل انتقال ابرمتن امن) یا گواهی‌های SSL در اکثر موارد با رمزگذاری RSA ایمن می‌شوند. یک سیستم رمزنگاری RSA برای رمزگذاری ایمیل ها، پیام رسان های دیجیتال، داده های تصویری یا هارد دیسک نیز مناسب است. از آنجایی که رمزگشایی حتی در بالاترین توان محاسباتی بدون کلید RSA ضروری زمان زیادی می برد، این روش نسبتاً ایمن در نظر گرفته می شود.

در بسیاری از موارد، یک سیستم رمزنگاری RSA با روش‌های دیگر رمزگذاری ترکیب می‌شود تا اطمینان حاصل شود که محتوا یا داده‌ها نمی‌توانند بدون مجوز باز یا خوانده شوند. حتی اگر وب سایت خود را به SSL تبدیل کنید، در بیشتر موارد از ترکیبی از رمزگذاری های مختلف استفاده می شود.

امضای دیجیتال با استفاده از رمزگذاری RSA

علاوه بر رمزگذاری RSA، که برای مثال در پروتکل های SSL یا TLS استفاده می شود، این تکنیک برای ایجاد یک امضای دیجیتال نیز مناسب است. برای تأیید صحت یک پیام یا فایل، و همچنین برای اطمینان از اینکه فایل متعاقباً ویرایش نشده است، امضا با استفاده از کلید خصوصی RSA ایجاد می‌شود. سپس می توان از کلید عمومی برای بررسی اینکه آیا امضا و فایل مربوطه همچنان مطابقت دارند یا خیر استفاده می شود.

امنیت و حملات RSA
مانند بسیاری از سیستم های رمزنگاری، امنیت RSA به نحوه پیاده سازی و استفاده از آن بستگی دارد. یکی از عوامل مهم اندازه کلید است. هرچه تعداد بیت‌ها در یک کلید بیشتر باشد (در اصل چقدر طول کلید است)، شکستن آن از طریق حملاتی مانند brute-forcing و factoring دشوارتر است.

از آنجایی که الگوریتم‌های کلید نامتقارن مانند RSA را می‌توان با فاکتورسازی اعداد صحیح شکست، در حالی که الگوریتم‌های کلید متقارن مانند AES را نمی‌توان، کلیدهای RSA برای دستیابی به همان سطح امنیتی باید بسیار طولانی‌تر باشند.

در حال حاضر، بزرگترین اندازه کلیدی که فاکتور گرفته شده است 768 بیت است. این کار توسط تیمی از دانشگاهیان طی دو سال و با استفاده از صدها ماشین انجام شد.

از آنجایی که فاکتورگیری تا پایان سال 2009 تکمیل شد و قدرت محاسباتی از آن زمان به طور قابل توجهی افزایش یافته است، می توان فرض کرد که تلاشی با شدت مشابه اکنون می تواند کلید RSA بسیار بزرگتری را فاکتور نماید.

با وجود این، زمان و منابع مورد نیاز برای این نوع حمله، آن را از دسترس بیشتر هکرها خارج کرده و وارد قلمرو دولت‌های ملی می‌کند. بهترین طول کلید برای استفاده به مدل تهدید فردی شما بستگی دارد. مؤسسه ملی استاندارد و فناوری حداقل اندازه کلید 2048 بیتی را توصیه می کند، اما کلیدهای 4096 بیتی نیز در برخی شرایط که سطح تهدید بالاتر است استفاده می شود.

فاکتورینگ تنها یکی از راه هایی است که می توان RSA را شکست. تعدادی از حملات دیگر پتانسیل شکستن رمزگذاری را با مقدار کمتری از منابع دارند، اما اینها به پیاده سازی و عوامل دیگر بستگی دارد، نه لزوما خود RSA. برخی از این موارد عبارتند از:

آیا اعداد اول واقعا تصادفی هستند؟
برخی از پیاده سازی های RSA از مولدهای اعداد تصادفی ضعیف جهت بدست آوردن اعداد اول استفاده می کنند. اگر این اعداد به اندازه کافی تصادفی نباشند، فاکتورگیری آنها و شکستن رمزگذاری برای مهاجمان بسیار آسان تر می شود. این مشکل را می توان با استفاده از یک تولید کننده اعداد شبه تصادفی ایمن رمزنگاری شده اجتناب کرد.

تولید کلید ضعیف
کلیدهای RSA برای اینکه ایمن باشند باید در پارامترهای خاصی قرار بگیرند. اگر اعداد اول p و q خیلی نزدیک به هم باشند، کلید به راحتی قابل کشف است. به همین ترتیب، عدد d که بخشی از کلید خصوصی را تشکیل می دهد، نمی تواند خیلی کوچک باشد. مقادیر کوچک حل آن را آسان می کند. مهم است که طول این اعداد برای ایمن نگه داشتن کلید شما کافی باشد.

حملات کانال جانبی Side channel

نوعی حمله هستند که مستقیماً RSA را از بین نمی برند، بلکه از اطلاعات پیاده سازی آن جهت ارائه نکاتی در مورد فرآیند رمزگذاری به مهاجمان اطلاع می دهند. این حملات می توانند شامل مواردی مانند تجزیه و تحلیل میزان توان مورد استفاده یا تجزیه و تحلیل پیش بینی شاخه باشد که از اندازه گیری زمان اجرا جهت کشف کلید خصوصی استفاده می نماید.

نوع دیگری از حمله کانال جانبی به عنوان حمله زمان شناخته می شود. اگر مهاجم توانایی اندازه‌گیری زمان رمزگشایی در رایانه هدف خود را برای تعدادی از پیام‌های رمزگذاری شده مختلف داشته باشد، این اطلاعات می‌تواند این امکان را برای مهاجم فراهم کند که از کلید خصوصی هدف مطمئن شود.

اکثر پیاده سازی های RSA با افزودن یک مقدار یکباره در طول فرآیند رمزگذاری، از این حمله جلوگیری می کنند، که این همبستگی را حذف می کند. این فرآیند کور کردن رمزنگاری یا cryptographic blinding نامیده می شود.

آیا رمزگذاری RSA برای آینده ایمن است؟

خبر خوب این است که با وجود این حملات احتمالی، RSA در حال حاضر جهت استفاده ایمن در نظر گرفته می شود. اخطار این است که باید به درستی اجرا شود و از کلیدی استفاده شود که در پارامترهای صحیح قرار می گیرد. همانطور که قبلاً بحث کردیم، پیاده‌سازی‌هایی که از padding استفاده نمی‌کنند، از اعداد اولیه با اندازه نامناسب استفاده می‌کنند یا آسیب‌ پذیری‌ های دیگری دارند، نمی‌توانند ایمن در نظر گرفته شوند.

اگر می خواهید از رمزگذاری RSA استفاده نمایید، مطمئن شوید که از یک کلید حداقل 1024 بیتی استفاده می کنید. کسانی که مدل‌های تهدید بالاتری دارند، اگر می‌خواهند با اطمینان از RSA استفاده کنند، باید از کلیدهای 2048 یا 4096 بیتی استفاده کنند.

تا زمانی که از نقاط ضعف RSA آگاه باشید و از آن به درستی استفاده کنید، باید از RSA برای اشتراک گذاری کلید و سایر کارهای مشابه که نیاز به رمزگذاری کلید عمومی دارند، احساس امنیت نمایید.

در حالی که RSA در حال حاضر ایمن است، انتظار می رود افزایش محاسبات کوانتومی چالش هایی را در آینده ایجاد نماید.

آموزش شبکه